Artikel Rekayasa dan Manajemen Sistem (SE&M) memberikan praktik terbaik siklus hidup sistem untuk mendefinisikan dan melaksanakan proses interdisipliner guna memastikan bahwa kebutuhan pelanggan terpenuhi dengan kinerja teknis, jadwal, dan solusi yang sesuai dengan biaya. Gambar di bawah ini menggambarkan konteks proses SE&M dan panduan praktik dalam SEBoK.

^{_{Sumber: sebokwiki.org}}

^{_{Gambar 1: Konteks SE&M SEBoK Bagian 3 [SEBoK Asli] untuk lebih jelasnya lihat Struktur SEBoK}}

Materi SE&M saat ini sedang diperbarui untuk memberikan panduan implementasi Rekayasa Digital [DE] dan Rekayasa Sistem Berbasis Model [MBSE] bagi para praktisi desain sistem yang menggunakan Bahasa Pemodelan Sistem (SysML).

• DE melakukan pengembangan sistem-perangkat lunak Agile berdasarkan standar terbuka industri dengan menggunakan MBSE.
• MBSE mengembangkan dan mengintegrasikan model desain SysML dengan kemampuan simulasi untuk kolaborasi lintas domain di seluruh siklus hidup.
• SysML adalah notasi grafis standar industri dengan semantik formal (makna) untuk mendefinisikan persyaratan sistem, batasan, alokasi, perilaku dan karakteristik struktur

Artikel SE&M memberikan contoh proses dan praktik yang dapat disesuaikan bagi organisasi teknik untuk memenuhi tujuan bisnis strategis dan tujuan proyek individu termasuk:

• Bagaimana teknik melakukan pengembangan sistem
• Tujuan dari setiap artefak teknik yang dihasilkan
• Bagaimana sistem diintegrasikan, dan persyaratan diverifikasi
• Bagaimana desain produk baru dialihkan ke operasi produksi
• Bagaimana sistem yang dihasilkan digunakan dan dipertahankan untuk memenuhi kebutuhan pelanggan

Tinjauan rekayasa dan manajemen sistem

Peran Rekayasa Sistem [SE] adalah mendefinisikan persyaratan sistem, batasan, alokasi, perilaku, dan karakteristik struktur untuk memenuhi kebutuhan pelanggan. Sistem didefinisikan dalam hal elemen struktural hirarkis dan interaksi perilakunya. Interaksi tersebut meliputi pertukaran data, energi, gaya, atau massa yang memodifikasi keadaan elemen-elemen yang bekerja sama sehingga menghasilkan perilaku yang muncul, diskrit, atau kontinu. Perilaku tersebut berada pada tingkat agregasi berurutan [bottoms-up] atau dekomposisi [top-down] untuk memenuhi persyaratan, kendala, dan alokasi. SE berkolaborasi dalam tim produk terintegrasi dengan teknik kelistrikan, mekanik, perangkat lunak, dan teknik khusus untuk menentukan implementasi desain rinci subsistem dan komponen untuk mengembangkan solusi teknis yang menyeluruh.

SE secara tradisional menerapkan praktik-praktik spesifik domain yang intuitif yang menekankan pada proses dan prosedur dengan kemampuan menulis yang baik untuk mengatur informasi secara manual dalam kumpulan dokumen yang berbeda termasuk spesifikasi kebutuhan sistem tekstual, laporan analisis, deskripsi desain sistem, dan spesifikasi antarmuka. SE tradisional sering disebut sebagai pendekatan yang berpusat pada dokumen. Praktisi desain sistem telah mengembangkan teknik berbasis model sejak akhir 1990-an untuk memfasilitasi komunikasi, mengelola kompleksitas desain, meningkatkan kualitas produk, meningkatkan penangkapan dan penggunaan kembali pengetahuan. MBSE didefinisikan sebagai aplikasi formal pemodelan grafis dengan definisi semantik yang tepat untuk analisis operasional, definisi persyaratan, pengembangan desain sistem, dan kegiatan verifikasi yang dimulai pada fase konseptual dan berlanjut di seluruh fase siklus hidup selanjutnya [INCOSE, 2015]. MBSE melakukan pengembangan sistem dengan menggunakan ekosistem rekayasa yang terdiri dari alat yang tersedia secara komersial untuk membuat model desain sistem dengan semantik yang sesuai dengan SysML yang merepresentasikan persyaratan sistem, batasan, alokasi, perilaku, dan karakteristik struktur. Model desain sistem ini menyediakan Sumber Kebenaran Otoritatif [ASoT] untuk dasar teknis proyek dengan kemampuan simulasi ujung ke ujung yang terintegrasi untuk mengevaluasi parameter kinerja utama sistem dalam lingkungan komputasi digital. MBSE mencakup pembuatan, pengembangan, dan pemanfaatan model desain digital dengan analisis khusus produk domain termasuk kedirgantaraan, mobil, konsumen, pertahanan, dan perangkat lunak.

Adopsi praktik DE baru-baru ini [Roper, 2020] memperluas transformasi MBSE berdasarkan prinsip-prinsip berikut:

• Pengembangan Sistem dan Perangkat Lunak Tangkas untuk memprioritaskan pengembangan kemampuan dan merespons ancaman, lingkungan, dan tantangan yang terus berkembang.
• Modular Open System Approach [MOSA] untuk mengembangkan lini produk berdasarkan standar industri yang dapat beradaptasi dengan kebutuhan pelanggan yang terus berkembang dengan kapabilitas baru, yang dimodifikasi, dan yang sudah ada [reuse].
• Digital Engineering [DE] untuk mengembangkan, mengintegrasikan, dan menggunakan model desain MBSE dengan kemampuan simulasi untuk meniru sistem dalam lingkungan komputasi digital secara realistis untuk kolaborasi lintas domain di seluruh siklus pengembangan, verifikasi, produksi, dan keberlanjutan desain sistem.

Model desain sistem mencakup representasi desain sistem fungsional, logis, dan fisik dengan kemampuan yang terintegrasi dengan disiplin ilmu kelistrikan, mekanik, perangkat lunak, dan desain khusus untuk penilaian fungsional dan kinerja sistem. Skrip model desain dapat mengekspor spesifikasi fungsional (SSS, B1, B2, B5), spesifikasi antarmuka (IRS, ICD, IDD), laporan penelusuran desain & persyaratan, dan deskripsi desain (SADD, SSDD, SWDD). Simulasi terintegrasi menyediakan kembaran digital dengan utas digital dari parameter kinerja utama sistem untuk mengevaluasi alternatif desain dalam lingkungan komputasi digital untuk menemukan dan menyelesaikan cacat desain sebelum mengeluarkan biaya untuk memproduksi prototipe fisik.

• Thread digital adalah kerangka kerja analitis yang menyediakan simulasi sistem ujung ke ujung untuk mengevaluasi operasi logis dan parameter kinerja utama di lingkungan komputasi digital dengan bertukar informasi antara alat pemodelan teknik yang berbeda di seluruh siklus hidup. Evaluasi simulasi thread digital memastikan bahwa persyaratan, interaksi, dan ketergantungan dipahami secara umum di seluruh disiplin ilmu teknik. Perubahan desain secara otomatis tercermin dalam semua penggunaan model desain untuk menilai kepatuhan, dengan masalah apa pun yang ditandai untuk tindakan perbaikan.
• Digital twins adalah representasi otoritatif dari sistem fisik termasuk koneksi ujung-ke-ujung utas digital dengan semua data, model, dan infrastruktur yang diperlukan untuk mendefinisikan dan mengoptimalkan siklus hidup sistem secara digital. Digital twins memungkinkan kolaborasi tim proyek, penilaian kinerja fungsional simulasi sistem, evaluasi dampak perubahan desain, dan perpustakaan penggunaan kembali manajemen lini produk

MBSE meningkatkan kemampuan untuk menangkap, menganalisis, berbagi, dan mengelola informasi otoritatif yang terkait dengan spesifikasi lengkap suatu produk dibandingkan dengan pendekatan berbasis dokumen tradisional. MBSE menyediakan kemampuan untuk mengkonsolidasikan informasi dalam sumber yang dapat diakses dan terpusat, memungkinkan otomatisasi sebagian atau keseluruhan dari banyak proses rekayasa sistem, dan memfasilitasi representasi interaktif dari komponen dan perilaku sistem. Materi SE&M yang lama semuanya terpengaruh oleh adopsi praktik MBSE, dan SEBoK memperbarui materinya untuk mencerminkan praktik dan prinsip terbaik dalam lingkungan rekayasa berbasis model yang terintegrasi.  Materi yang diperbarui untuk menentukan perilaku sistem dan karakteristik struktur dengan penelusuran ke persyaratan terkait disusun sesuai dengan Standar Proses Siklus Hidup Sistem ISO/IEC/IEEE-15288:2015 yang ditunjukkan pada gambar di bawah ini.

^{_{Sumber: sebokwiki.org}}

^{_{Gambar 2. Garis Besar Standar ISO/IEC/IEEE-15288:2015 (SEBoK Asli)}}

Gambar 3 menggambarkan contoh umum dari proses desain sistem berbasis model. Pendekatan ini konsisten dengan panduan Buku Pegangan Rekayasa Sistem INCOSE dengan penambahan repositori model desain sistem untuk mengelola dasar teknis proyek. Proses desain MBSE tidak bergantung pada metodologi desain tertentu (misalnya, analisis terstruktur, berorientasi objek, dll.) yang digunakan. Setiap elemen model desain memiliki definisi tunggal dengan beberapa contoh pada berbagai diagram yang menggambarkan struktur sistem dan karakteristik perilaku termasuk penelusuran ke persyaratan terkait. Proses desain berbasis model dapat disesuaikan untuk proyek-proyek yang bergantung pada pendekatan domain-area, pengembangan, dan siklus hidup.

^{_{Sumber: sebokwiki.org}}

^{_{Gambar 3: Proses Rekayasa Sistem Berbasis Model. (Sumber: SEBoK Original)}}

Pengetahuan dan keahlian desain sistem domain-area produk masih wajib dimiliki dengan penerapan pendekatan MBSE, yang menggunakan alat bantu pemodelan terintegrasi sebagai pengganti alat bantu gambar lawas (misalnya, Powerpoint, Visio), spesifikasi berbasis teks (misalnya, DOORS), dan laporan analisis rekayasa dan deskripsi desain (Word).

Panduan desain sistem berbasis model SE&M memungkinkan tim multidisiplin untuk mengelola garis dasar teknis proyek dalam satu model desain sistem yang tunggal, konsisten, dan tidak ambigu. Model desain MBSE yang terintegrasi berisi representasi fungsional dan logis sistem dengan implementasi desain rinci fisik untuk menentukan, menganalisis, merancang, dan memverifikasi bahwa persyaratan telah terpenuhi. Panduan ini mendefinisikan konvensi untuk mengembangkan model desain untuk menentukan perilaku sistem dan karakteristik struktur dengan penelusuran ke persyaratan proyek. Model desain menyediakan sumber informasi otoritatif digital untuk repositori informasi kebenaran untuk dasar teknis proyek. Simulasi model dengan kasus uji memfasilitasi verifikasi desain awal dalam lingkungan komputasi digital untuk menemukan dan menyelesaikan cacat desain sebelum mengeluarkan biaya untuk memproduksi prototipe fisik.

Praktik MBSE mengubah SE dari pendekatan berbasis dokumen saat ini menjadi penggunaan alat bantu desain berbantuan komputer yang sebanding dengan evolusi disiplin EE, ME, SW, dan SP beberapa tahun yang lalu. Manfaat nilai tambah adalah penggunaan alat pemodelan terintegrasi alih-alih alat gambar statis tradisional [misalnya, PowerPoint, Visio] untuk pengembangan produk, integrasi, dan verifikasi di seluruh siklus hidup sistem. Panduan desain sistem berbasis model SE&M memberikan praktik terbaik MBSE untuk menerapkan strategi rekayasa digital guna mengembangkan model desain sistem untuk menentukan dan mensimulasikan karakteristik perilaku/struktur dengan ketertelusuran ke persyaratan terkait berdasarkan prinsip-prinsip berikut:

1. Mengembangkan, mengintegrasikan, dan menggunakan model desain sistem digital untuk kolaborasi lintas domain di seluruh siklus hidup produk [yaitu, pengembangan teknik, produksi, dan keberlanjutan].
2. Mengelola lini produk berdasarkan standar terbuka industri dengan pustaka varian khusus yang disesuaikan untuk pelanggan dengan kemampuan desain sistem yang baru, dimodifikasi, dan yang sudah ada [penggunaan ulang].
3. Memelihara repositori informasi sumber kebenaran otoritatif digital untuk setiap varian produk yang telah disetujui secara teknis di seluruh siklus hidup produk untuk memfasilitasi kolaborasi dan menginformasikan pengambilan keputusan.
4. Melakukan simulasi model dengan kasus uji verifikasi untuk mengevaluasi perilaku dan struktur sistem dalam lingkungan komputasi digital untuk menemukan cacat desain sebelum biaya produksi prototipe fisik.
5. Mendefinisikan utas digital dari parameter kinerja utama teknis dan menyinkronkan informasi di seluruh alat pemodelan desain SE, EE, ME, SW, dan SP untuk memastikan persyaratan, interaksi, dan ketergantungan sistem dipahami secara umum. Perubahan desain secara otomatis tercermin dalam semua penggunaan model di seluruh alat bantu disiplin teknik dan dinilai kesesuaiannya, dengan masalah apa pun yang ditandai untuk tindakan perbaikan.
6. Memanfaatkan proses pengembangan “Agile” untuk menyediakan metode yang konsisten dalam mengembangkan model desain sistem dan mengidentifikasi utas digital untuk sinkronisasi data di seluruh disiplin ilmu teknik dalam lingkungan teknik berbasis model yang terintegrasi.

Pendekatan desain sistem berbasis model SE&M memiliki landasan ilmiah teoretis berdasarkan fenomena sistem yang didefinisikan oleh Prinsip Hamilton: sebuah sistem terdiri dari elemen-elemen hirarkis yang berinteraksi dengan cara bertukar data, energi, gaya, atau massa untuk mengubah keadaan elemen yang bekerja sama yang menghasilkan perilaku yang muncul, diskrit, atau kontinu pada tingkat agregasi atau dekomposisi yang progresif seperti yang ditunjukkan pada Gambar 4.

^{_{Sumber: sebokwiki.org}}

^{_{Gambar 4: Fenomena Sistem - Prinsip Hamilton. (Sumber: SEBoK Original)}}

Disadur dari: sebokwiki.org

Bagaimana perbandingannya dengan teknik mekatronika?
Dalam teknik desain sistem, fokus pada semester awal adalah membangun dasar pengetahuan teknik umum, serta pengetahuan dan pengalaman dengan metodologi desain yang dapat diterapkan secara luas. Mahasiswa kemudian dapat mengambil pilihan teknis dan mengerjakan proyek-proyek desain tingkat lanjut di bidang-bidang yang menjadi minat mereka, seperti mekatronika, sistem cerdas, interaksi manusia-komputer, pemodelan sistem, dan energi alternatif.

Sebaliknya, program teknik mekatronika berfokus secara khusus pada desain sistem mekatronika yang efektif yang menggabungkan konsep mekanik, elektronik, komputer, dan perangkat lunak, seperti robotika, sistem kendaraan, dan perangkat “pintar”.

Bagi siswa yang tertarik pada aplikasi luas desain dan sistem mekatronika, pendekatan terbaik mungkin adalah menggabungkan program Desain Sistem dengan Opsi Mekatronika.

Bagaimana perbandingannya dengan rekayasa komputer, sistem, dan perangkat lunak?
Program-program di bidang teknik komputer dan teknik sistem berfokus hampir secara eksklusif pada sistem komputasi (perangkat keras/perangkat lunak), sedangkan Desain Sistem mencakup berbagai macam sistem yang jauh lebih luas yang mungkin atau mungkin tidak termasuk sistem komputasi. Demikian pula, program rekayasa perangkat lunak Waterloo berfokus hampir secara eksklusif pada pengembangan perangkat lunak.

Banyak mahasiswa desain sistem menemukan diri mereka dalam pekerjaan yang berorientasi pada perangkat lunak (pemrograman), terutama selama masa kerja awal. Namun, mahasiswa kami tidak terikat untuk mengikuti jalur yang hanya berorientasi pada komputer atau perangkat lunak.

Mahasiswa mengambil sekitar satu mata kuliah berbasis komputer per semester selama dua tahun pertama masa studi, setelah itu mereka dapat memilih untuk mengambil mata kuliah pilihan yang terkait dengan komputer dan perangkat lunak, atau berkonsentrasi pada bidang-bidang seperti sistem ergonomi-manusia dan sosial-lingkungan. Proyek desain senior mencakup berbagai aplikasi, pemodelan sistem lingkungan, analisis konflik, pengenalan pola, sistem cerdas, interaksi manusia-komputer, dan biomekanik.

Bagaimana jika dibandingkan dengan manajemen dan teknik industri?

Teknik industri secara tradisional berfokus pada penerapan metode teknik untuk peningkatan proses manufaktur dan industri, namun telah diperluas untuk mencakup domain terkait pekerjaan lainnya seperti perawatan kesehatan dan manajemen informasi. Ini adalah fokus program teknik manajemen Waterloo, yang ditawarkan oleh Departemen Ilmu Manajemen kami.

Rekayasa desain sistem mencakup banyak metode teknik industri sebagai bagian dari kurikulum inti, seperti penjadwalan dan optimasi, faktor manusia dan ergonomi, manajemen informasi, dan manajemen proyek, yang diterapkan dalam proyek desain tim tahun pertama siswa. Namun, siswa kami juga mempelajari dasar-dasar disiplin ilmu mekanik, listrik, komputasi, sipil, dan rekayasa perangkat lunak, yang memungkinkan mereka menentukan di mana mereka memfokuskan studi mereka di tahun-tahun atas.

Disadur dari: uwaterloo.ca

Python, bahasa pemrograman yang ditafsirkan dan tingkat tinggi, telah menjadi salah satu bahasa pemrograman yang paling populer di dunia sejak dirilis pada tahun 1991 oleh Guido van Rossum. Filosofi desain Python menitikberatkan pada keterbacaan kode dan penggunaan spasi putih yang signifikan, membuatnya menjadi pilihan yang ideal untuk proyek-proyek skala kecil maupun besar.

Salah satu keunggulan Python adalah kemampuannya dalam menangani berbagai paradigma pemrograman, termasuk pemrograman terstruktur, berorientasi objek, dan fungsional. Dikenal sebagai bahasa "termasuk baterai", Python dilengkapi dengan perpustakaan standar yang luas, memungkinkan pengguna untuk mengakses berbagai fungsi dan alat tanpa perlu menginstal tambahan.

Sejak dirilisnya Python 2.0 pada tahun 2000, bahasa ini telah mengalami beberapa pembaruan signifikan, termasuk fitur-fitur seperti pemahaman daftar dan sistem pengumpulan sampah yang lebih canggih. Pada tahun 2008, Python 3.0 diperkenalkan sebagai revisi utama, meskipun tidak sepenuhnya kompatibel dengan versi sebelumnya. Hal ini membutuhkan modifikasi pada kode Python 2 untuk dapat berjalan pada Python 3.

Python memiliki keunggulan dalam ketersediaannya untuk berbagai sistem operasi. Implementasi referensi Python, yang dikenal sebagai CPython, dikembangkan dan dipelihara oleh komunitas pemrogram global. Python Software Foundation, sebuah organisasi nirlaba, bertanggung jawab atas pengelolaan dan pengembangan sumber daya Python dan CPython.

Sebagai salah satu bahasa pemrograman paling populer di dunia, Python secara konsisten menduduki peringkat teratas dalam daftar bahasa pemrograman yang diminati oleh para pengembang. Keunggulan Python dalam keterbacaan kode, fleksibilitas, dan kemampuan yang luas menjadikannya pilihan yang sangat dihargai dalam berbagai industri dan proyek pengembangan perangkat lunak.

Sejarah dan Filosofi Python

Python, bahasa pemrograman yang diciptakan pada akhir 1980-an oleh Guido van Rossum di Belanda, merupakan kelanjutan dari bahasa ABC dan memiliki kemampuan untuk menangani pengecualian serta berinteraksi dengan sistem operasi Amoeba. Implementasinya dimulai pada bulan Desember 1989, dengan van Rossum sebagai pengembang utama hingga Juli 2018, ketika dia mengumumkan "liburan permanen" dari tanggung jawabnya sebagai Benevolent Dictator For Life Python. Python 2.0 dirilis pada tahun 2000 dengan berbagai fitur baru, termasuk pengumpul sampah pendeteksian siklus dan dukungan untuk Unicode.

Tanggal akhir penggunaan Python 2.7 awalnya dijadwalkan pada tahun 2015, namun ditunda hingga tahun 2020 karena banyaknya kode yang tidak dapat dengan mudah dilanjutkan ke Python 3. Pada 2022, perilisan Python 3.10.4 dan 3.9.12 dipercepat karena masalah keamanan, sementara versi 3.6 dan yang lebih lama tidak lagi didukung. Python memperoleh popularitasnya sebagai salah satu bahasa pemrograman paling populer.

Python adalah bahasa pemrograman multi-paradigma, mendukung pemrograman berorientasi objek, terstruktur, fungsional, dan berorientasi aspek. Desainnya menawarkan dukungan untuk pemrograman fungsional dalam tradisi Lisp dengan fungsi seperti filter, map, dan reduce, serta pemahaman daftar, kamus, set, dan ekspresi generator. Filosofi Python diuraikan dalam dokumen The Zen of Python, menekankan nilai-nilai seperti kecantikan, keterbacaan, dan kesederhanaan.

Python dirancang untuk menjadi sangat dapat dikembangkan dan modular, dengan perpustakaan standar yang besar dan penerjemah yang mudah diperluas. Visi van Rossum terhadap bahasa inti kecil dengan perpustakaan yang luas berasal dari pengalamannya dengan bahasa ABC. Python juga dikenal karena pendekatannya yang menyenangkan dan ramah pengguna, tercermin dalam namanya yang terinspirasi oleh grup komedi Inggris Monty Python.

Pengguna dan penggemar Python sering disebut sebagai Pythonistas, dan bahasa ini terus berkembang dengan komunitas yang kuat di belakangnya. Dengan sejarah yang kaya dan filosofi yang kuat, Python tetap menjadi salah satu bahasa pemrograman yang paling diminati dan dipilih oleh pengembang di seluruh dunia.

Sintaks dan Semantik Python

Python dikenal sebagai bahasa pemrograman yang mudah dibaca dan dipahami. Sintaksnya bersih dan tidak berantakan secara visual, sering menggunakan kata kunci bahasa Inggris daripada tanda baca. Berbeda dengan bahasa lain seperti C atau Pascal, Python tidak menggunakan tanda kurung awal untuk membatasi blok, dan pernyataan titik koma setelahnya bersifat opsional.

Indentasi adalah kunci dalam Python, menggunakan spasi untuk membatasi blok kode. Peningkatan indentasi menandakan awal blok, sedangkan penurunan indentasi menandakan akhir blok. Ini memastikan bahwa struktur visual program mencerminkan struktur semantiknya dengan akurat.

Python menawarkan beragam pernyataan dan kontrol aliran, termasuk if, else, elif, for, while, try, except, raise, class, def, with, break, continue, pass, assert, yield, dan import. Pernyataan-pernyataan ini memberikan fleksibilitas dalam menulis kode dan menangani pengecualian, iterasi, dan banyak lagi.

Python juga memiliki konsep metode pada objek, yang memungkinkan fungsi yang dilampirkan ke kelas objek. Penulisan kode Python menganut prinsip duck typing, memungkinkan variabel tanpa tipe yang ditentukan tetapi objek yang diketik. Operasi aritmatika seperti penambahan, pengurangan, perkalian, dan pembagian dapat dilakukan dengan mudah menggunakan simbol yang terintegrasi dalam bahasa.

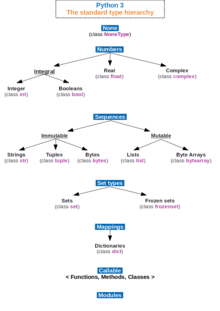
_{Hierarki tipe standar di Python 3}

Dengan kesederhanaan sintaks dan semantiknya, Python menjadi pilihan yang populer di kalangan pengembang. Keterbacaan dan kemudahan penggunaan membuatnya menjadi bahasa yang ideal untuk berbagai proyek, dari yang sederhana hingga yang kompleks. Dengan Python, kompleksitas kode dapat dikurangi tanpa mengorbankan fungsionalitas, menjadikannya salah satu bahasa pemrograman yang paling diminati dan digunakan di seluruh dunia.

Disadur dari: id.wikipedia.org/wiki/Python

Transformasi data merupakan inti dari komputasi, yang berfungsi sebagai saluran yang melaluinya informasi berevolusi dari satu format atau struktur ke format lainnya. Proses ini merupakan bagian integral dari berbagai tugas yang berhubungan dengan data, termasuk integrasi data, penyimpanan data, dan integrasi aplikasi.

Kompleksitas transformasi data dapat sangat bervariasi, tergantung pada tingkat perubahan yang diperlukan antara data sumber dan data target. Sementara beberapa transformasi mungkin sangat mudah, yang lain membutuhkan manipulasi yang rumit. Biasanya, transformasi data memadukan langkah-langkah manual dan otomatis untuk mencapai hasil yang diinginkan. Alat dan teknologi yang digunakan untuk transformasi data sangat beragam, yang mencerminkan beragamnya format, struktur, kompleksitas, dan volume data yang mengalami transformasi.

Salah satu bentuk transformasi data yang penting adalah penyusunan ulang data master. Di sini, seluruh basis data mengalami transformasi atau penyusunan ulang tanpa perlu mengekstrak data. Dalam database yang dirancang dengan baik, semua data dihubungkan secara langsung atau tidak langsung ke sekumpulan tabel database master melalui batasan kunci asing.

Dengan menyusun ulang tabel-tabel basis data master ini dengan indeks unik yang berbeda, baik data yang terkait secara langsung maupun tidak langsung juga diubah. Meskipun ada transformasi ini, bentuk asli data tetap dapat diakses melalui indeks unik yang ada. Sangat penting untuk menjalankan penyusunan ulang database ini dengan cermat untuk menghindari dampak buruk pada arsitektur perangkat lunak.Dalam skenario di mana pemetaan data terjadi secara tidak langsung melalui model data yang memediasi, proses ini disebut sebagai mediasi data.

Proses Perjalanan Transformasi Data

Transformasi data adalah proses penting dalam bidang pengelolaan data, yang mencakup beberapa langkah penting yang disesuaikan dengan kompleksitas transformasi yang ada. Mari kita selidiki setiap langkah untuk memahami signifikansinya dalam narasi transformasi yang lebih luas.

1. Penemuan Data:
Perjalanannya dimulai dengan penemuan data, di mana alat pembuatan profil atau skrip manual mengungkap seluk-beluk struktur dan karakteristik data. Langkah mendasar ini meletakkan dasar untuk memahami bagaimana data harus dibentuk dan dibentuk agar selaras dengan tujuan transformasi.

2. Pemetaan Data:
Di sini, masing-masing bidang menjalani pemetaan, modifikasi, penggabungan, pemfilteran, atau agregasi untuk membentuk hasil akhir. Biasanya dipelopori oleh pengembang atau analis teknis yang berpengalaman dalam teknologi transformasi, pemetaan data menetapkan cetak biru perjalanan transformasi.

3. Pembuatan Kode:
Prosesnya beralih ke pembuatan kode, di mana instruksi yang dapat dieksekusi, seperti SQL, Python, atau R, dibuat berdasarkan aturan pemetaan yang telah ditentukan sebelumnya. Teknologi transformasi memainkan peran penting di sini, memanfaatkan metadata atau definisi yang disediakan oleh pengembang untuk menghasilkan kode yang diperlukan.

4. Eksekusi Kode:
Dengan kode di tangan, saatnya untuk mengeksekusi. Baik terintegrasi secara mulus dalam alat transformasi atau memerlukan intervensi manual dari pengembang, eksekusi kode menghidupkan proses transformasi, mengarahkan data menuju kondisi yang diharapkan.

5. Tinjauan Data:
Pengembaraan transformasi mencapai puncaknya pada peninjauan data, yang hasilnya diperiksa dengan cermat untuk memastikan keselarasan dengan tujuan transformasi. Biasanya dipimpin oleh pengguna bisnis atau pengguna akhir, langkah ini mengungkap anomali atau kesalahan apa pun, menandakan perbaikan atau persyaratan baru bagi pengembang atau analis.

Menjelajahi Transformasi Data: Batch vs Interaktif

Transformasi data telah lama menjadi proses fundamental dalam dunia manajemen data, dan hadir dalam dua bentuk utama: batch dan interaktif. Mari kita pelajari setiap jenisnya untuk memahami signifikansi dan implikasinya dalam ranah integrasi data.

• Transformasi Data Batch:

Secara tradisional, transformasi data telah beroperasi sebagai proses massal atau batch, di mana pengembang atau ahli teknis menulis kode atau menentukan aturan transformasi dalam alat integrasi data. Aturan-aturan ini kemudian dieksekusi pada volume data yang besar, mengikuti serangkaian langkah linier yang telah ditentukan sebelumnya. Transformasi data batch berfungsi sebagai tulang punggung berbagai teknologi integrasi data, termasuk pergudangan data, migrasi, dan integrasi aplikasi.

• Manfaat dan Keterbatasan:

Meskipun transformasi data batch telah membuktikan nilainya selama bertahun-tahun, transformasi data batch memiliki manfaat dan keterbatasan. Di satu sisi, hal ini memungkinkan pemrosesan volume data yang sangat besar, memberi makan aplikasi penting dan penyimpanan data. Akan tetapi, hal ini juga menimbulkan tantangan. Sebagai contoh, pengguna bisnis sering kali tidak berperan langsung dalam proses transformasi, yang menyebabkan potensi salah tafsir terhadap persyaratan dan bertambahnya waktu untuk mendapatkan solusi. Hal ini memicu kebutuhan akan kelincahan dan layanan mandiri dalam integrasi data, yang bertujuan untuk memberdayakan pengguna agar dapat mentransformasi data secara interaktif.

• Transformasi Data Interaktif:

Masukkan transformasi data interaktif (IDT), sebuah kemampuan baru yang merevolusi lanskap transformasi data. Tidak seperti transformasi batch, IDT memungkinkan analis bisnis dan pengguna untuk berinteraksi langsung dengan kumpulan data yang besar melalui antarmuka visual yang intuitif. Antarmuka ini memfasilitasi pemahaman, koreksi, dan manipulasi data melalui interaksi sederhana seperti mengklik atau memilih elemen data. Perusahaan seperti Trifacta, Alteryx, dan Paxata menawarkan alat transformasi data interaktif, mengabstraksikan kerumitan teknis dan memberdayakan pengguna untuk mengontrol data mereka.

• Manfaat dan Implikasi:

Solusi transformasi data interaktif menyederhanakan proses persiapan data, mengurangi waktu yang dibutuhkan untuk mentransformasi data dan menghilangkan kesalahan yang merugikan dalam interpretasi. Dengan menghilangkan pengembang dari persamaan, sistem ini menempatkan kekuatan di tangan pengguna bisnis dan analis, memungkinkan mereka untuk berinteraksi dan memanipulasi data sesuai kebutuhan. Visualisasi dalam antarmuka membantu dalam mengidentifikasi pola dan anomali, yang selanjutnya meningkatkan pemahaman data dan pengambilan keputusan.

Bahasa Transformasional

Dalam bidang transformasi data, terdapat banyak bahasa yang dirancang khusus untuk tujuan ini. Bahasa-bahasa ini sering kali memerlukan tata bahasa terstruktur, biasanya menyerupai bentuk Backus–Naur (BNF), untuk memfasilitasi penggunaannya. Mari kita jelajahi beberapa bahasa transformasional yang menonjol dan signifikansinya dalam lanskap transformasi data.

1. AWK: Sebagai salah satu bahasa transformasi data tekstual tertua dan terpopuler, AWK telah teruji oleh waktu, menawarkan kemampuan yang kuat untuk memanipulasi data.
2. Perl: Terkenal karena fleksibilitasnya, Perl berfungsi sebagai bahasa tingkat tinggi yang mampu melakukan operasi yang kuat pada data biner dan teks, menjadikannya pilihan yang disukai banyak pengembang.
3. Bahasa Templat: Bahasa-bahasa ini berspesialisasi dalam mengubah data menjadi dokumen, memenuhi kebutuhan pembuatan dan pemrosesan dokumen.
4. TXL: Dengan fokus pada pembuatan prototipe, TXL menawarkan deskripsi berbasis bahasa yang ideal untuk mengubah kode sumber atau data secara efisien.
5. XSLT: Berfungsi sebagai bahasa transformasi data XML standar, XSLT dapat diterapkan secara luas di berbagai domain, menyediakan transformasi data XML yang mulus.

• Bahasa Transformasi Khusus Domain (DSL):

Perusahaan seperti Trifacta dan Paxata telah memelopori pengembangan DSL yang dirancang khusus untuk melayani dan mengubah kumpulan data. DSL ini, seperti "Wrangle" dari Trifacta, menyederhanakan proses transformasi dan meningkatkan produktivitas, khususnya bagi pengguna non-teknis.

• Keuntungan DSL:

Salah satu keuntungan utama DSL adalah kemampuannya untuk mengabstraksi logika eksekusi yang mendasarinya, memungkinkan integrasi yang lancar dengan berbagai mesin pemrosesan seperti Spark, MapReduce, dan Dataflow. Tidak seperti bahasa tradisional, DSL tidak terikat pada mesin dasar tertentu, sehingga menawarkan fleksibilitas dan skalabilitas dalam operasi transformasi data.

Disadur dari: en.wikipedia.org/wiki/Data_transformation_(computing)

Analitika prediktif adalah bentuk analitika bisnis yang menerapkan pembelajaran mesin untuk menghasilkan model prediktif untuk berbagai aplikasi bisnis. Ini mencakup berbagai teknik statistik dari pemodelan prediktif dan pembelajaran mesin yang menganalisis fakta-fakta saat ini dan historis untuk membuat prediksi tentang peristiwa masa depan atau yang tidak diketahui lainnya. Ini merupakan subset utama dari aplikasi pembelajaran mesin; dalam beberapa konteks, hal ini sinonim dengan pembelajaran mesin.

Dalam bisnis, model prediktif memanfaatkan pola yang ditemukan dalam data historis dan transaksional untuk mengidentifikasi risiko dan peluang. Model-model ini menangkap hubungan antara banyak faktor untuk memungkinkan penilaian risiko atau potensi yang terkait dengan satu set kondisi tertentu, membimbing pengambilan keputusan untuk transaksi kandidat.

Efek fungsional yang menentukan dari pendekatan teknis ini adalah bahwa analitika prediktif menyediakan skor prediktif (probabilitas) untuk setiap individu (pelanggan, karyawan, pasien perawatan kesehatan, SKU produk, kendaraan, komponen, mesin, atau unit organisasi lainnya) untuk menentukan, memberi informasi, atau mempengaruhi proses organisasi yang berlaku pada sejumlah besar individu, seperti dalam pemasaran, penilaian risiko kredit, deteksi penipuan, manufaktur, perawatan kesehatan, dan operasi pemerintah termasuk penegakan hukum.

Definisi Analitika Prediktif: Analitika prediktif adalah seperangkat teknologi intelijen bisnis (BI) yang mengungkapkan hubungan dan pola dalam volume data besar yang dapat digunakan untuk memprediksi perilaku dan peristiwa. Berbeda dengan teknologi BI lainnya, analitika prediktif melihat ke depan, menggunakan peristiwa masa lalu untuk memprediksi masa depan. Teknik statistik analitika prediktif meliputi pemodelan data, pembelajaran mesin, kecerdasan buatan, algoritma pembelajaran mendalam, dan penambangan data. Seringkali, peristiwa yang tidak diketahui yang menarik minat berada di masa depan, tetapi analitika prediktif dapat diterapkan pada jenis yang tidak diketahui apa pun, baik itu terjadi di masa lalu, sekarang, atau di masa depan. Misalnya, mengidentifikasi tersangka setelah suatu kejahatan telah terjadi, atau penipuan kartu kredit saat itu terjadi. Inti dari analitika prediktif bergantung pada penangkapan hubungan antara variabel-variabel penjelas dan variabel yang diprediksi dari kejadian-kejadian masa lalu, dan memanfaatkannya untuk memprediksi hasil yang tidak diketahui. Namun, penting untuk dicatat bahwa akurasi dan kegunaan hasil akan sangat bergantung pada tingkat analisis data dan kualitas asumsi.

Analitika prediktif sering didefinisikan sebagai prediksi pada tingkat granularitas yang lebih detail, yaitu, menghasilkan skor prediktif (probabilitas) untuk setiap elemen organisasi individu. Hal ini membedakannya dari peramalan. Misalnya, "Analitika prediktif—Teknologi yang belajar dari pengalaman (data) untuk memprediksi perilaku masa depan individu untuk menghasilkan keputusan yang lebih baik." Dalam sistem industri masa depan, nilai dari analitika prediktif akan diprediksi dan mencegah masalah potensial untuk mencapai nol-kegagalan dan lebih lanjut akan terintegrasi ke dalam analitika preskriptif untuk optimasi keputusan.

Teknik Analitik untuk Memprediksi Data

Dalam dunia analitik, terdapat beragam pendekatan dan teknik yang digunakan untuk melakukan prediksi data, yang dapat dikelompokkan ke dalam teknik regresi dan teknik pembelajaran mesin.

• Pembelajaran Mesin

Pembelajaran mesin dapat didefinisikan sebagai kemampuan mesin untuk belajar dan meniru perilaku manusia yang memerlukan kecerdasan. Hal ini dicapai melalui kecerdasan buatan, algoritma, dan model.

• Model ARIMA

Model ARIMA adalah contoh umum dari model deret waktu. Model ini menggunakan autoregresi, yang berarti model dapat disesuaikan dengan perangkat lunak regresi yang akan menggunakan pembelajaran mesin untuk melakukan sebagian besar analisis regresi dan smoothing. Model ARIMA dikenal tidak memiliki tren keseluruhan, tetapi memiliki variasi di sekitar rata-rata yang memiliki amplitudo konstan, menghasilkan pola waktu yang secara statistik serupa. Melalui ini, variabel dianalisis dan data disaring untuk lebih memahami dan memprediksi nilai masa depan.

• Model Deret Waktu

Model deret waktu adalah subset dari pembelajaran mesin yang memanfaatkan deret waktu untuk memahami dan meramalkan data menggunakan nilai-nilai masa lalu. Deret waktu adalah urutan nilai variabel selama periode yang sama, seperti tahun atau kuartal dalam aplikasi bisnis. Untuk mencapai ini, data harus dihaluskan, atau varians acak dari data harus dihilangkan untuk mengungkapkan tren dalam data.

• Model Prediktif

Model Prediktif adalah teknik statistik yang digunakan untuk memprediksi perilaku masa depan. Ini menggunakan model prediktif untuk menganalisis hubungan antara unit spesifik dalam sampel yang diberikan dan satu atau lebih fitur unit tersebut. Tujuan dari model-model ini adalah untuk menilai kemungkinan bahwa unit dalam sampel lain akan menampilkan pola yang sama.

• Analisis Regresi

Secara umum, analisis regresi menggunakan data struktural bersama dengan nilai-nilai masa lalu dari variabel independen dan hubungan antara mereka dan variabel dependen untuk membentuk prediksi.

• Regresi Linier

Dalam regresi linier, sebuah plot dibangun dengan nilai-nilai sebelumnya dari variabel dependen yang dipetakan pada sumbu Y dan variabel independen yang sedang dianalisis dipetakan pada sumbu X. Garis regresi kemudian dibangun oleh program statistik yang mewakili hubungan antara variabel independen dan dependen yang dapat digunakan untuk memprediksi nilai-nilai variabel dependen berdasarkan variabel independen. Dengan garis regresi, program juga menunjukkan persamaan intercept kemiringan untuk garis yang mencakup tambahan untuk istilah kesalahan regresi, di mana semakin tinggi nilai istilah kesalahan, semakin tidak presisi model regresi. Untuk mengurangi nilai istilah kesalahan, variabel independen lainnya diperkenalkan ke dalam model, dan analisis serupa dilakukan pada variabel independen tersebut.

Penerapan Analitik Prediktif dalam Bidang Bisnis

Analisis prediktif merupakan bagian penting dari analisis bisnis yang menggunakan pembelajaran mesin untuk membuat model prediktif untuk berbagai aplikasi bisnis. Dalam konteks audit, tinjauan analitik digunakan untuk mengevaluasi keberagaman saldo akun yang dilaporkan. Proses ini melibatkan penggunaan metode seperti ARIMA dan analisis regresi untuk membentuk prediksi yang disebut ekspektasi bersyarat dari saldo yang sedang diaudit. Metode STAR juga digunakan untuk melakukan tinjauan analitik dengan menggunakan analisis regresi. Penyerapan prosedur analitis ke dalam standar audit menyoroti kebutuhan untuk menyesuaikan metodologi ini sesuai dengan data yang spesifik.

Kesimpulannya, analisis prediktif telah menjadi elemen penting dalam berbagai bidang bisnis dan industri. Dengan memanfaatkan data historis dan teknik prediktif, perusahaan dapat merencanakan strategi, mengambil keputusan yang lebih baik, dan meningkatkan efisiensi operasional. Dari manajemen aset hingga perlindungan anak, serta prediksi arus kas hingga keputusan hukum, analisis prediktif memberikan beragam manfaat yang dapat membantu perusahaan mencapai tujuan mereka dengan lebih baik. Dengan adopsi teknologi ini, perusahaan dapat mengoptimalkan kinerja mereka, meningkatkan keuntungan, dan memberikan layanan yang lebih baik kepada pelanggan mereka.

Disadur dari: en.wikipedia.org

Penambangan teks, juga dikenal sebagai analisis teks atau penambangan data teks (TDM), adalah metode untuk mengekstraksi wawasan yang berharga dari sumber teks. Proses ini melibatkan penggunaan algoritme komputer untuk mengungkap informasi baru dari berbagai materi tertulis seperti situs web, email, buku, dan artikel. Tujuannya adalah untuk mendapatkan informasi berkualitas tinggi dengan mengidentifikasi pola dan tren melalui teknik pembelajaran pola statistik.

Menurut Hotho dkk. (2005), text mining dapat dikategorikan ke dalam tiga perspektif: ekstraksi informasi, data mining, dan penemuan pengetahuan dalam database (KDD). Ekstraksi informasi biasanya mencakup penataan teks input, mendapatkan pola dari data terstruktur, dan mengevaluasi serta menginterpretasikan hasilnya. Istilah "kualitas tinggi" dalam text mining mengacu pada relevansi, kebaruan, dan ketertarikan informasi yang diekstrak.

Tugas-tugas umum dalam text mining meliputi kategorisasi teks, pengelompokan, ekstraksi konsep, analisis sentimen, peringkasan, dan pemodelan relasi entitas. Analisis teks melibatkan berbagai teknik seperti analisis leksikal, pengenalan pola, penandaan, ekstraksi informasi, penggalian data, visualisasi, dan analisis prediktif. Tujuan utamanya adalah mengubah teks menjadi data yang dapat dianalisis menggunakan pemrosesan bahasa alami (NLP) dan berbagai algoritme.

Aplikasi khas dari text mining adalah untuk menganalisis koleksi dokumen dalam bahasa alami, baik untuk tujuan klasifikasi prediktif atau untuk mengekstrak informasi untuk populasi database atau pengayaan indeks pencarian. Dalam proses ini, dokumen berfungsi sebagai unit dasar dari data tekstual, yang ditemukan dalam berbagai jenis koleksi.

Analisis Teks: Memahami Informasi dari Sumber Teks untuk Bisnis dan Penelitian

Analisis teks menggambarkan seperangkat teknik linguistik, statistik, dan pembelajaran mesin yang memodelkan dan mengatur konten informasi dari sumber-sumber teks untuk kecerdasan bisnis, analisis data eksploratif, penelitian, atau investigasi. Istilah ini hampir sinonim dengan penambangan teks; bahkan, Ronen Feldman memodifikasi deskripsi "penambangan teks" pada tahun 2000 menjadi "analisis teks" pada tahun 2004. Istilah terakhir ini kini lebih sering digunakan dalam pengaturan bisnis sementara "penambangan teks" digunakan dalam beberapa area aplikasi terawal, yang berasal dari tahun 1980-an, terutama penelitian ilmu kehidupan dan intelijen pemerintah.

Istilah analisis teks juga menggambarkan aplikasi analisis teks untuk menanggapi masalah-masalah bisnis, baik secara mandiri maupun bersamaan dengan pencarian dan analisis data numerik. Sebuah kebenaran umum bahwa 80 persen informasi yang relevan dengan bisnis berasal dalam bentuk yang tidak terstruktur, terutama teks. Teknik dan proses ini menemukan dan menyajikan pengetahuan – fakta, aturan bisnis, dan hubungan – yang terkunci dalam bentuk teks, sulit untuk diproses secara otomatis.

Proses Analisis Teks

Subtugas—komponen dari usaha analisis teks yang lebih besar—biasanya mencakup:

• Reduksi dimensi adalah teknik penting untuk pra-pemrosesan data. Teknik ini digunakan untuk mengidentifikasi kata dasar untuk kata-kata aktual dan mengurangi ukuran data teks.
• Pemulihan informasi atau identifikasi sebuah korpus adalah langkah persiapan: mengumpulkan atau mengidentifikasi sekumpulan materi teks, di Web atau disimpan dalam sistem file, database, atau manajer korpus konten, untuk analisis.
• Meskipun beberapa sistem analisis teks menerapkan secara eksklusif metode statistik canggih, banyak yang lain menerapkan pemrosesan bahasa alami yang lebih luas, seperti tagging bagian ucapan, analisis sintaksis, dan jenis analisis linguistik lainnya.
• Pengenalan entitas bernama adalah penggunaan daftar istilah atau teknik statistik untuk mengidentifikasi fitur teks bernama: orang, organisasi, nama tempat, simbol saham, singkatan tertentu, dan sebagainya.
• Disambiguasi—penggunaan petunjuk kontekstual—mungkin diperlukan untuk memutuskan di mana, misalnya, "Ford" dapat merujuk pada mantan presiden AS, produsen kendaraan, bintang film, sungai, atau entitas lainnya.
• Pengenalan Pola Entitas yang Diidentifikasi: Fitur seperti nomor telepon, alamat email, jumlah (dengan unit) dapat dikenali melalui pencocokan pola atau pencocokan pola lainnya.
• Pengelompokan dokumen: identifikasi set dokumen teks yang serupa.
• Coreference: identifikasi frasa benda dan istilah lain yang merujuk pada objek yang sama.
• Ekstraksi Hubungan, Fakta, dan Peristiwa: identifikasi asosiasi di antara entitas dan informasi lain dalam teks.
• Analisis sentimen melibatkan membedakan materi subjektif (dibandingkan dengan faktual) dan mengekstrak berbagai bentuk informasi sikap: sentimen, pendapat, suasana hati, dan emosi. Teknik analisis teks membantu menganalisis sentimen pada tingkat entitas, konsep, atau topik dan membedakan pemegang pendapat dan objeknya.
• Analisis teks kuantitatif adalah seperangkat teknik yang berasal dari ilmu sosial di mana baik seorang hakim manusia atau komputer mengekstrak hubungan semantik atau tata bahasa antara kata-kata untuk menemukan makna atau pola gaya, biasanya, teks personal kasual untuk tujuan profil psikologis, dll.
• Pra-pemrosesan biasanya melibatkan tugas-tugas seperti tokenisasi, penyaringan, dan stemming.

Penerapan Teknologi Penambangan Teks 

Teknologi penambangan teks kini secara luas diterapkan dalam berbagai kebutuhan pemerintahan, penelitian, dan bisnis. Semua kelompok ini dapat menggunakan penambangan teks untuk manajemen catatan dan mencari dokumen yang relevan dengan kegiatan sehari-hari mereka. Profesional hukum misalnya, dapat menggunakan penambangan teks untuk e-discovery. Pemerintah dan kelompok militer menggunakan penambangan teks untuk kepentingan keamanan nasional dan intelijen. Para peneliti ilmiah menggabungkan pendekatan penambangan teks ke dalam upaya untuk mengorganisir set data teks besar (yaitu, mengatasi masalah data yang tidak terstruktur), untuk menentukan gagasan-gagasan yang disampaikan melalui teks (misalnya, analisis sentimen di media sosial), dan untuk mendukung penemuan ilmiah di bidang ilmu kehidupan dan bioinformatika. Di dunia bisnis, aplikasi digunakan untuk mendukung intelijen kompetitif dan penempatan iklan otomatis, di antara banyak kegiatan lainnya.

• Aplikasi Keamanan
• Aplikasi Biomedis
• Aplikasi Perangkat Lunak
• Aplikasi Media Online
• Aplikasi Bisnis dan Pemasaran
• Analisis Sentimen
• Penambangan Literatur Ilmiah dan Aplikasi Akademis
• Ilmu Digital dan Sosiologi Komputasi

Teknologi penambangan teks telah membuka peluang baru yang luas untuk berbagai kebutuhan, dari keamanan hingga bisnis, menawarkan cara yang efektif untuk mengelola, menganalisis, dan memanfaatkan informasi yang terkandung dalam teks. Dengan kemampuannya untuk menggali wawasan dari data yang tidak terstruktur, penambangan teks memberikan kontribusi yang berharga bagi kemajuan di berbagai bidang dan sektor.

Dampak Teknologi Penambangan Teks dalam Pencarian dan Analisis Konten

Hingga baru-baru ini, pencarian berbasis teks yang paling umum digunakan oleh situs web hanya dapat menemukan dokumen yang mengandung kata-kata atau frasa yang ditentukan pengguna. Namun, dengan penggunaan web semantik, penambangan teks sekarang dapat menemukan konten berdasarkan makna dan konteks (bukan hanya berdasarkan kata-kata tertentu). Selain itu, perangkat lunak penambangan teks dapat digunakan untuk membangun catatan besar informasi tentang orang dan peristiwa tertentu.

Misalnya, dataset besar berdasarkan data yang diekstraksi dari laporan berita dapat dibangun untuk memfasilitasi analisis jaringan sosial atau kontra-intelijen. Secara efektif, perangkat lunak penambangan teks dapat berperan dalam kapasitas yang mirip dengan analis intelijen atau pustakawan riset, meskipun dengan cakupan analisis yang lebih terbatas. Penambangan teks juga digunakan dalam beberapa filter spam email sebagai cara untuk menentukan karakteristik pesan yang kemungkinan adalah iklan atau materi yang tidak diinginkan lainnya. Penambangan teks memainkan peran penting dalam menentukan sentimen pasar keuangan.

Disadur dari: en.wikipedia.org/wiki