Ketidakpastian atau Ketidakyakinan (Incertitude) mengacu pada situasi epistemik yang melibatkan informasi yang tidak sempurna atau tidak diketahui. Hal ini berlaku untuk prediksi kejadian di masa depan, pengukuran fisik yang telah dilakukan, atau hal yang tidak diketahui. Ketidakpastian muncul dalam lingkungan yang sebagian dapat diamati atau lingkungan yang bersifat stokastik, serta karena ketidaktahuan, kemalasan, atau keduanya. Ketidakpastian muncul di sejumlah bidang, termasuk asuransi, filsafat, fisika, statistik, ekonomi, keuangan, kedokteran, psikologi, sosiologi, teknik, metrologi, meteorologi, ekologi, dan ilmu informasi.
Konsep
Meskipun istilah-istilah tersebut digunakan dalam berbagai cara di kalangan masyarakat umum, banyak ahli teori keputusan, statistik, dan bidang kuantitatif lainnya yang mendefinisikan ketidakpastian, risiko, dan pengukurannya sebagai:
Ketidakpastian
Kurangnya kepastian, suatu keadaan dengan pengetahuan yang terbatas di mana tidak mungkin untuk secara tepat menggambarkan keadaan yang ada, hasil di masa depan, atau lebih dari satu hasil yang mungkin terjadi.
Pengukuran ketidakpastian
Sekumpulan kemungkinan keadaan atau hasil di mana probabilitas ditetapkan untuk setiap kemungkinan keadaan atau hasil - ini juga mencakup penerapan fungsi kepadatan probabilitas pada variabel kontinu.
Ketidakpastian tingkat kedua
Dalam statistik dan ekonomi, ketidakpastian orde dua direpresentasikan dalam fungsi kepadatan probabilitas atas probabilitas (orde satu). Opini dalam logika subjektif mengandung ketidakpastian jenis ini.
Risiko adalah keadaan ketidakpastian, di mana beberapa hasil yang mungkin terjadi memiliki efek yang tidak diinginkan atau kerugian yang signifikan. Pengukuran risiko mencakup serangkaian ketidakpastian yang terukur, di mana beberapa hasil yang mungkin terjadi adalah kerugian, dan besarnya kerugian tersebut. Ini juga mencakup fungsi kerugian atas variabel kontinu.
Ketidakpastian versus variabilitas
Ada perbedaan antara ketidakpastian dan variabilitas. Ketidakpastian dikuantifikasi dengan distribusi probabilitas yang bergantung pada pengetahuan tentang kemungkinan nilai tunggal yang benar dari kuantitas yang tidak pasti. Variabilitas dikuantifikasi dengan distribusi frekuensi dari beberapa contoh kuantitas, yang berasal dari data yang diamati.
Ketidakpastian Knightian
Dalam ilmu ekonomi, pada tahun 1921 Frank Knight membedakan ketidakpastian dari risiko dengan ketidakpastian sebagai kurangnya pengetahuan yang tidak dapat diukur dan tidak mungkin dihitung. Karena tidak adanya statistik yang didefinisikan dengan jelas dalam sebagian besar keputusan ekonomi di mana orang menghadapi ketidakpastian, ia percaya bahwa kita tidak dapat mengukur probabilitas dalam kasus-kasus seperti itu; ini sekarang disebut sebagai ketidakpastian Knightian.
Ketidakpastian harus dipahami dalam arti yang sangat berbeda dari pengertian risiko yang sudah dikenal, yang tidak pernah dipisahkan dengan benar. Fakta yang penting adalah bahwa 'risiko' dalam beberapa kasus berarti kuantitas yang dapat diukur, sementara di lain waktu merupakan sesuatu yang jelas bukan merupakan karakter ini; dan ada perbedaan yang sangat besar dan krusial dalam hal fenomena yang bergantung pada mana yang benar-benar ada dan beroperasi.... Akan terlihat bahwa ketidakpastian yang dapat diukur, atau 'risiko' yang tepat, seperti yang akan kita gunakan dalam istilah ini, sangat jauh berbeda dengan ketidakpastian yang tidak dapat diukur, sehingga pada dasarnya bukan merupakan ketidakpastian sama sekali. - Frank Knight (1885-1972), Risiko, Ketidakpastian, dan Keuntungan (1921), Universitas Chicago.
Ada perbedaan mendasar antara imbalan untuk mengambil risiko yang diketahui dan mengambil risiko yang nilainya tidak diketahui. Hal ini sangat mendasar, bahkan... risiko yang diketahui tidak akan menghasilkan imbalan atau pembayaran khusus sama sekali. - Frank Knight
Knight menunjukkan bahwa hasil yang tidak menguntungkan dari risiko yang diketahui dapat diasuransikan selama proses pengambilan keputusan karena memiliki distribusi probabilitas yang jelas. Risiko yang tidak diketahui tidak memiliki distribusi probabilitas yang diharapkan, yang dapat menyebabkan keputusan perusahaan yang sangat berisiko.
Taksonomi ketidakpastian dan keputusan lainnya mencakup pengertian ketidakpastian yang lebih luas dan bagaimana hal itu harus didekati dari perspektif etika:
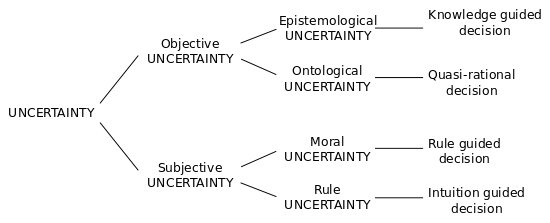
Sebuah taksonomi ketidakpastian.
Risiko dan ketidakpastian
Sebagai contoh, jika tidak diketahui apakah besok akan turun hujan atau tidak, maka terdapat ketidakpastian. Jika probabilitas diterapkan pada hasil yang mungkin terjadi dengan menggunakan prakiraan cuaca atau bahkan hanya penilaian probabilitas yang dikalibrasi, maka ketidakpastian telah dikuantifikasi. Misalkan saja, peluang matahari akan bersinar sebesar 90%. Jika ada acara besar dan mahal yang direncanakan di luar ruangan besok, maka ada risiko karena ada 10% kemungkinan hujan, dan hujan tidak diinginkan. Lebih jauh lagi, jika ini adalah acara bisnis dan $100.000 akan hilang jika hujan turun, maka risikonya sudah dikuantifikasi (10% kemungkinan kehilangan $100.000). Situasi ini dapat dibuat lebih realistis dengan mengkuantifikasi hujan ringan vs hujan lebat, biaya penundaan vs pembatalan, dll.
Beberapa orang mungkin merepresentasikan risiko dalam contoh ini sebagai "kerugian peluang yang diharapkan" (EOL) atau peluang kerugian dikalikan dengan jumlah kerugian (10% × $ 100.000 = $ 10.000). Hal ini berguna jika penyelenggara acara "netral terhadap risiko", yang mana kebanyakan orang tidak demikian. Sebagian besar orang akan bersedia membayar premi untuk menghindari kerugian. Sebuah perusahaan asuransi, misalnya, akan menghitung EOL sebagai nilai minimum untuk perlindungan asuransi apa pun, kemudian menambahkan biaya operasional dan keuntungan lainnya. Karena banyak orang bersedia membeli asuransi karena berbagai alasan, maka jelas EOL saja bukanlah nilai yang dirasakan untuk menghindari risiko.
Ketidakpastian Radikal
Istilah 'ketidakpastian radikal' diciptakan oleh John Kay dan Mervyn King dalam buku mereka yang berjudul Radical Uncertainty: Pengambilan Keputusan untuk Masa Depan yang Tidak Dapat Diketahui, yang diterbitkan pada bulan Maret 2020. Ketidakpastian ini berbeda dengan ketidakpastian Knightian, berdasarkan apakah ketidakpastian tersebut 'dapat diselesaikan' atau tidak. Jika ketidakpastian muncul dari kurangnya pengetahuan, dan kurangnya pengetahuan tersebut dapat diselesaikan dengan memperoleh pengetahuan (seperti melalui penelitian primer atau sekunder), maka hal tersebut bukanlah ketidakpastian radikal. Hanya ketika tidak ada cara yang tersedia untuk memperoleh pengetahuan yang dapat menyelesaikan ketidakpastian, maka ketidakpastian tersebut dianggap 'radikal'.
Dalam pengukuran
Prosedur yang paling umum digunakan untuk menghitung ketidakpastian pengukuran dijelaskan dalam "Panduan Ekspresi Ketidakpastian dalam Pengukuran" (GUM) yang diterbitkan oleh ISO. Karya turunannya misalnya National Institute of Standards and Technology (NIST) Technical Note 1297, "Panduan untuk Mengevaluasi dan Mengekspresikan Ketidakpastian Hasil Pengukuran NIST", dan publikasi Eurachem/Citac "Menghitung Ketidakpastian dalam Pengukuran Analitik". Ketidakpastian hasil pengukuran umumnya terdiri dari beberapa komponen. Komponen-komponen tersebut dianggap sebagai variabel acak, dan dapat dikelompokkan ke dalam dua kategori sesuai dengan metode yang digunakan untuk memperkirakan nilai numeriknya:
- Tipe A, yang dievaluasi dengan metode statistik
- Tipe B, yang dievaluasi dengan cara lain, misalnya dengan menetapkan distribusi probabilitas
Dengan menyebarkan varians komponen melalui fungsi yang menghubungkan komponen dengan hasil pengukuran, ketidakpastian pengukuran gabungan diberikan sebagai akar kuadrat dari varians yang dihasilkan. Bentuk yang paling sederhana adalah deviasi standar dari pengamatan berulang.
Dalam metrologi, fisika, dan teknik, ketidakpastian atau margin kesalahan pengukuran, ketika dinyatakan secara eksplisit, diberikan oleh rentang nilai yang kemungkinan besar mencakup nilai sebenarnya. Hal ini dapat dilambangkan dengan batang kesalahan pada grafik, atau dengan notasi berikut:
- nilai terukur ± ketidakpastian
- nilai terukur + ketidakpastian -ketidakpastian
- nilai terukur (ketidakpastian)
Pada notasi terakhir, tanda kurung adalah notasi ringkas untuk notasi ±. Sebagai contoh, menerapkan 10 1⁄2 meter dalam aplikasi ilmiah atau teknik, dapat ditulis 10,5 m atau 10,50 m, dengan konvensi yang berarti akurat dalam sepersepuluh meter, atau seperseratus. Ketepatannya simetris di sekitar angka terakhir. Dalam hal ini, setengah sepersepuluh ke atas dan setengah sepersepuluh ke bawah, jadi 10,5 berarti antara 10,45 dan 10,55. Dengan demikian dapat dipahami bahwa 10,5 berarti 10,5 ± 0,05, dan 10,50 berarti 10,50 ± 0,005, juga ditulis 10,50 (5) dan 10,500 (5). Tetapi, jika akurasinya dalam dua persepuluh, ketidakpastiannya adalah ± sepersepuluh, dan harus dituliskan secara eksplisit: 10,5±0,1 dan 10,50±0,01 atau 10,5 (1) dan 10,50 (1). Angka dalam tanda kurung berlaku untuk angka di sebelah kiri, dan bukan merupakan bagian dari angka tersebut, tetapi bagian dari notasi ketidakpastian. Angka-angka tersebut berlaku untuk angka yang paling tidak signifikan. Sebagai contoh, 1.00794(7) berarti 1.00794 ± 0.00007, sedangkan 1.00794(72) berarti 1.00794 ± 0.00072. Notasi ringkas ini digunakan sebagai contoh oleh IUPAC dalam menyatakan massa atom elemen.
Di media
Ketidakpastian dalam sains, dan ilmu pengetahuan secara umum, dapat ditafsirkan secara berbeda di ruang publik daripada di komunitas ilmiah. Hal ini sebagian disebabkan oleh keragaman audiens publik, dan kecenderungan para ilmuwan untuk salah memahami audiens awam sehingga tidak dapat mengkomunikasikan ide dengan jelas dan efektif. Salah satu contohnya dijelaskan oleh model defisit informasi. Selain itu, di ranah publik, sering kali ada banyak suara ilmiah yang memberikan masukan tentang satu topik.
Sebagai contoh, tergantung pada bagaimana sebuah isu dilaporkan di ranah publik, ketidaksesuaian antara hasil dari beberapa penelitian ilmiah karena perbedaan metodologi dapat ditafsirkan oleh publik sebagai kurangnya konsensus dalam situasi di mana konsensus sebenarnya ada. Interpretasi ini bahkan mungkin sengaja dipromosikan, karena ketidakpastian ilmiah dapat dikelola untuk mencapai tujuan tertentu. Sebagai contoh, para penyangkal perubahan iklim mengikuti saran Frank Luntz untuk membingkai pemanasan global sebagai isu ketidakpastian ilmiah, yang merupakan pendahulu dari bingkai konflik yang digunakan oleh para jurnalis ketika melaporkan isu tersebut.
Disadur dari: en.wikipedia.org